1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 static Random random = new Random ();public void sortArray (int [] nums) {int n = nums.length;if (n <= 1 ) {return ;0 , n - 1 );private void quickSort (int [] nums, int left, int right) {if (left >= right) {return ;int index = partition(nums, left, right);1 );1 , right);private int partition (int [] nums, int left, int right) {if (left >= right) {return left;int randomIndex = random.nextInt(right - left + 1 ) + left;int pivot = nums[left];int j = left;for (int i = left + 1 ; i <= right; i++) {if (nums[i] >= pivot) {continue ;else {return j;private void swap (int [] nums, int left, int right) {int tmp = nums[left];
使用 j 指针来收集小于等于 pivot 的元素,这个思想有些类似 283. 移动零 - 力扣(Leetcode) ,283 题的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public void moveZeroes (int [] nums) {int n = nums.length;int index = 0 ; for (int i = 0 ; i < n; i++) {if (nums[i] != 0 ) {for (int i = index; i < n; i++) {0 ;
为何要随机选择 pivot?
如果总是默认选择待排序区间的最左边元素作为枢轴的话,在有序区间上会导致递归树严重倾斜 。比如考虑序列 [1, 2, 3, 4, 5],每轮总是选择区间最左元素作为 pivot 的话,会导致每轮均无法找到小于 pivot 的元素,导致递归树倾斜
那么,是否确保 pivot 的随机性就足够了呢?考虑下面的序列 [2, 2, 2, 2],无论怎样随机选择枢轴,仍会导致递归树倾斜。所以单路快排在重复元素较多的序列上效果不佳,此时要用二路快排或是三路快排进行优化
左边:使用指针 le。遇到严格小于 pivot 的元素则将其放入左区间,否则停下(此时指向的元素是大于或者等于 pivot 的)
右边:使用指针 ge。遇到严格大于 pivot 的元素则将其放入右区间,否则停下(此时指向的元素是小于或者等于 pivot 的)
当 le >= ge 成立,遍历结束,将 pivot 放在 ge 的位置(多思考以下为什么。Key:遍历结束时,ge 要么在 le 的位置,要么在 le 的左边,此时 le 指向的元素才是小于等于 pivot 的)
le 和 ge 的初始值:根据我们的定义,[left+1, le) 是小于 pivot 的元素,(ge, right] 是大于 pivot 的元素,那么当 le 初始为 left + 1,ge 初始为 right 时,两个区间均为空
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 static Random random = new Random ();public void sortArray (int [] nums) {int n = nums.length;if (n <= 1 ) {return ;0 , n - 1 );private void quickSort (int [] nums, int left, int right) {if (left >= right) {return ;int index = partition(nums, left, right);1 );1 , right);private int partition (int [] nums, int left, int right) {if (left >= right) {return left;int randomIndex = random.nextInt(right - left + 1 ) + left;int pivot = nums[left];int le = left + 1 ;int ge = right;while (true ) {while (le <= ge && nums[le] < pivot) le++;while (le <= ge && nums[ge] > pivot) ge--;if (le >= ge) {break ;return ge;private void swap (int [] nums, int left, int right) {int tmp = nums[left];
下面是另一个版本的双指针对撞(来源于王道书,补充了随机选择 pivot),大体思路是一致的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 static Random random = new Random ();public void sortArray (int [] nums) {int n = nums.length;if (n <= 1 ) {return ;0 , n - 1 );private void quickSort (int [] nums, int left, int right) {if (left >= right) {return ;int index = partition(nums, left, right);1 );1 , right);private int partition (int [] nums, int left, int right) {int randomIndex = random.nextInt(right - left + 1 ) + left;int pivot = nums[left];while (left < right) {while (left < right && nums[right] >= pivot) right--; while (left < right && nums[left] <= pivot) left++; return left;private void swap (int [] nums, int left, int right) {int tmp = nums[left];
三路快排在解决荷兰国旗问题 时尤为有效,可以在 O ( n ) O(n) O ( n )
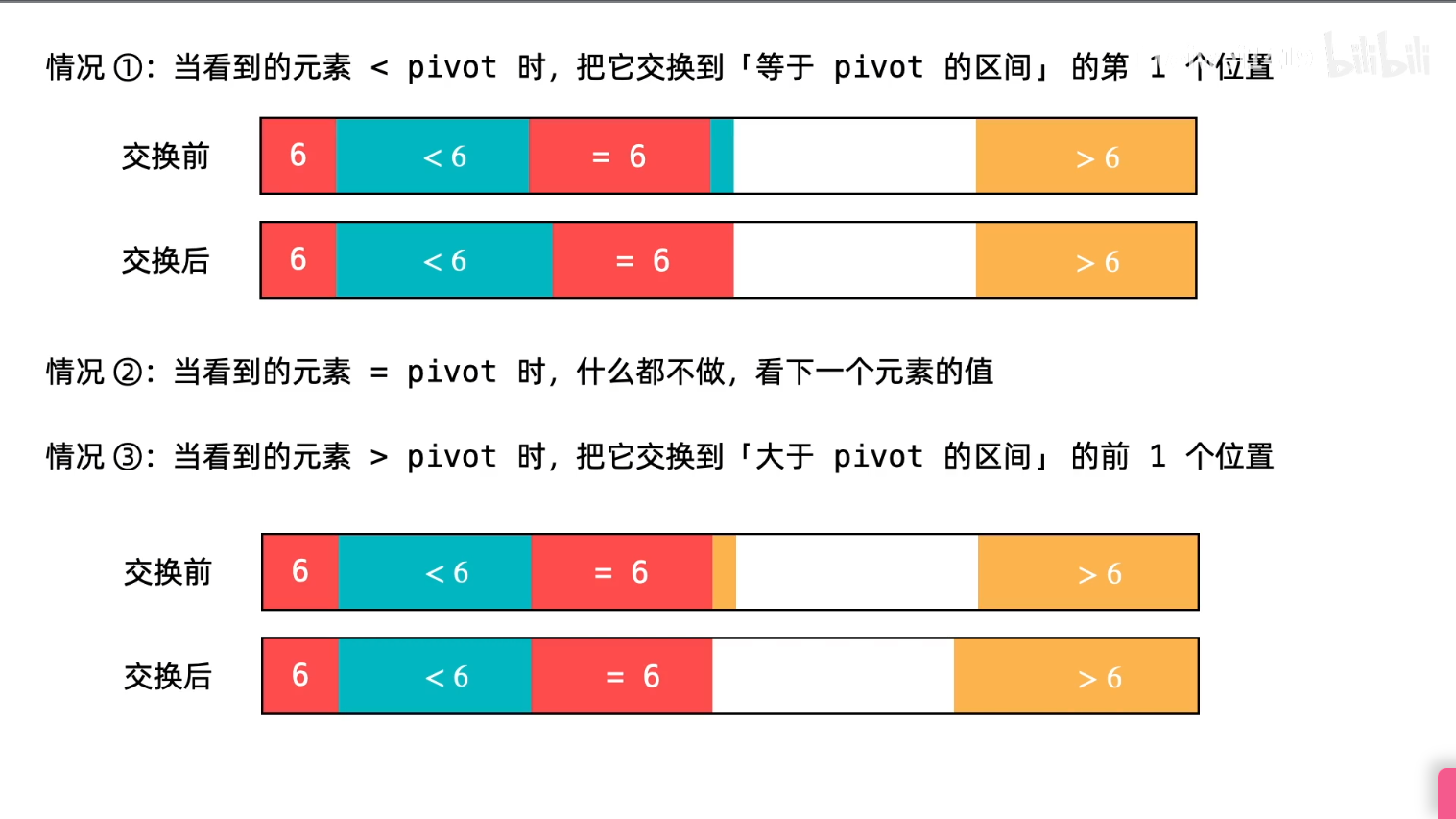
三路快排使用了三个区间,分别用来收集小于、等于和大于 pivot 的元素
区间定义如下:
[left+1, lt) < pivot
[lt, i) == pivot
(gt, right] > pivot
那么要如何初始 lt 和 gt 使得上面的三个区间均为空?
将 lt 初始为 left + 1,将 gt 初始为 right,i 初始为 left + 1。循环终止的条件是 i > gt,思考为何可以取等?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 static Random random = new Random ();public void sortArray (int [] nums) {int n = nums.length;0 , n - 1 );private void partition (int [] nums, int left, int right) {if (left >= right) {return ;int randomIndex = random.nextInt(right - left + 1 ) + left;int pivot = nums[left];int lt = left + 1 ;int gt = right;int i = left + 1 ;while (i <= gt) {if (nums[i] == pivot) {else if (nums[i] > pivot) {else {1 ); 2 );1 , right);private void swap (int [] nums, int left, int right) {int tmp = nums[left];
下面的题目均运用了快速排序的思想或是其子过程,在力扣上的标签是 快速选择知识点题库 - 力扣(LeetCode)
著名的荷兰国旗问题,使用三路快排可以在一趟扫描中解决
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class Solution {public void sortColors (int [] nums) {int n = nums.length;0 , n - 1 );private void partition (int [] nums, int left, int right) {if (left >= right) {return ;int index = -1 ;for (int i = left; i <= right; i++) {if (nums[i] == 1 ) {break ;if (index == -1 ) {int pivot = 1 ;int lt = left + 1 ;int gt = right;int i = left + 1 ;while (i <= gt) {if (nums[i] == 1 ) {else if (nums[i] == 2 ) {else {1 );private void swap (int [] nums, int left, int right) {int tmp = nums[left];
与单路快排的划分过程思路相似
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public int [] exchange(int [] nums) {int n = nums.length;int left = 0 ;int right = n - 1 ;while (left < right) {while (left < right && nums[left] % 2 == 1 ) left++;while (left < right && nums[right] % 2 == 0 ) right--;int tmp = nums[left];return nums;
经典的 TopK 问题,2016 年的 408 算法题中用到了同样的思路.
值得注意的是,数组中的第 K 小 的元素在下标的 k - 1 上(K 从 1 开始)
而数组中的第 K 大 的元素在下标的 length - k 上(K 从 1 开始)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 class Solution {static Random random = new Random ();public int findKthLargest (int [] nums, int k) {int n = nums.length;int index = -1 ;int left = 0 ;int right = n - 1 ;while (index != n - k) {if (index == n - k) {return nums[index];else if (index > n - k) {1 ;else {1 ;return -1 ;private int partition (int [] nums, int left, int right) {if (left >= right) {return left;int randomIndex = random.nextInt(right - left + 1 ) + left;int pivot = nums[left];int low = left;int high = right;while (low < high) {while (low < high && nums[high] >= pivot) {while (low < high && nums[low] <= pivot) {return low;private void swap (int [] nums, int left, int right) {int tmp = nums[left];
TopK 问题的变体,由于是选出 k 个数,因此还可以用堆解决
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public int [] getLeastNumbers(int [] arr, int k) {if (k == 0 ) {return new int [0 ];new PriorityQueue <>(new Comparator <Integer>() {public int compare (Integer o1, Integer o2) {return o2 - o1;for (int i = 0 ; i < k; i++) {10001 );for (int i = 0 ; i < arr.length; i++) {if (arr[i] < maxHeap.peek()) {int [] ans = new int [k];for (int i = 0 ; i < k; i++) {return ans;
效率很低😢
同样利用快速排序的子过程解决。由于有效的 k 从 1 开始,那么某次划分返回的 index 是 k - 1 的话,就找到最小的 k 个数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 class Solution {static Random random = new Random ();public int [] getLeastNumbers(int [] arr, int k) {if (k == 0 ) {return new int [0 ];int [] res = new int [k];int n = arr.length;int index = -1 ;int left = 0 ;int right = n - 1 ;while (index != k - 1 ) {if (index == k - 1 ) {for (int i = 0 ; i <= index; i++) {return res;else if (index > k - 1 ) {1 ;else {1 ;return null ;private int partition (int [] nums, int left, int right) {if (left >= right) {return left;int randomIndex = random.nextInt(right - left + 1 ) + left;int pivot = nums[left];while (left < right) {while (left < right && nums[right] >= pivot) {while (left < right && nums[left] <= pivot) {return left;private void swap (int [] nums, int left, int right) {int tmp = nums[left];
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 class Solution {static Random random = new Random ();public int [] topKFrequent(int [] nums, int k) {new HashMap <>();for (int num: nums) {0 ) + 1 );int n = cnts.keySet().size();int [] tmp = new int [n];int j = 0 ;for (int key: cnts.keySet()) {int index = -1 ;int left = 0 ;int right = n - 1 ;int [] ans = new int [k];while (index != n - k) {if (index == n - k) {for (int i = 0 ; i < k; i++) {return ans;else if (index > n - k) {1 ;else {1 ;return ans;private int partition (int [] nums, int left, int right) {if (left >= right) {return left;int randomIndex = random.nextInt(right - left + 1 ) + left;int pivot = nums[left];int pivotWeight = cnts.get(pivot);while (left < right) {while (left < right && cnts.get(nums[right]) >= pivotWeight) {while (left < right && cnts.get(nums[left]) <= pivotWeight) {return left;private void swap (int [] nums, int left, int right) {int tmp = nums[left];