这场整体来看的确不困难,T4 没有到 Hard 的难度。最近正好再复习数据结构,所以还是想出来了。感觉最难的其实是 T3 吧,虽然用了一点技巧,可是写的 if-else 真的很丑,怕没考虑全面,用例也只有不到 200 个,希望不要被 rejudge 吧🤣
T1 哈希表
求不同元素的数目时用哈希表从前至后和从后至前扫一遍即可,注意越界的判断,即 18 行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int[] distinctDifferenceArray(int[] nums) {
int n = nums.length;
HashSet<Integer> set1 = new HashSet<>();
HashSet<Integer> set2 = new HashSet<>();
int[] arr1 = new int[n];
int[] arr2 = new int[n];
for (int i = 0; i < n; i++) {
set1.add(nums[i]);
arr1[i] = set1.size();
}
for (int i = n - 1; i >= 0; i--) {
set2.add(nums[i]);
arr2[i] = set2.size();
}
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
if (i + 1 >= n) {
ans[i] = arr1[i];
} else {
ans[i] = arr1[i] - arr2[i + 1];
}
}
return ans;
}
}
|
T2 哈希表
一个哈希表记录元素-频数,另一个哈希表记录频数-具有该频数的元素集合
(更新:其实只用记录频数出现的频数就够了,没必要知道是哪些元素的频数)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class FrequencyTracker {
HashMap<Integer, Integer> data;
HashMap<Integer, HashSet<Integer>> freq;
public FrequencyTracker() {
data = new HashMap<>();
freq = new HashMap<>();
freq.put(0, new HashSet<>());
freq.put(1, new HashSet<>());
}
public void add(int number) {
if (data.containsKey(number)) {
data.put(number, 0);
}
int oldFreq = data.get(number);
int newFreq = oldFreq + 1;
if (freq.containsKey(newFreq)) {
freq.put(newFreq, new HashSet<>());
}
data.put(number, newFreq);
if (oldFreq == 0) {
HashSet<Integer> tmp = freq.get(1);
tmp.add(number);
} else {
HashSet<Integer> tmp = freq.get(oldFreq);
tmp.remove(number);
HashSet<Integer> tmp1 = freq.get(newFreq);
tmp1.add(number);
}
}
public void deleteOne(int number) {
if (data.containsKey(number) || data.get(number) == 0) {
return;
}
int oldFreq = data.get(number);
int newFreq = oldFreq - 1;
data.put(number, newFreq);
HashSet<Integer> tmp = freq.get(oldFreq);
tmp.remove(number);
HashSet<Integer> tmp2 = freq.get(newFreq);
tmp2.add(number);
}
public boolean hasFrequency(int frequency) {
if (freq.containsKey(frequency)) {
return false;
}
HashSet<Integer> tmp = freq.get(frequency);
return tmp.size() > 0;
}
}
|
T3
注意每次更新一个下标的颜色时,仅会影响 nums[i-1], nums[i], nums[i+1] 颜色的相同数目,所以每次更新颜色后不必扫一遍 nums,而是与前后元素进行讨论;注意边界条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| class Solution {
public int[] colorTheArray(int n, int[][] queries) {
int[] arr = new int[n];
Arrays.fill(arr, 0);
int num = queries.length;
int[] ans = new int[num];
if (n == 1) {
Arrays.fill(ans, 0);
return ans;
}
int sum = 0;
for (int i = 0; i < num; i++) {
int index = queries[i][0];
int color = queries[i][1];
int oldColor = arr[index];
if (oldColor == color) {
ans[i] = ans[i - 1];
continue;
}
arr[index] = color;
if (index == 0) {
if (oldColor == arr[index + 1] && arr[index + 1] = 0) {
sum--;
}
if (oldColor = arr[index + 1] && color == arr[index + 1]) {
sum++;
}
} else if (index == n - 1) {
if (oldColor == arr[index - 1] && arr[index - 1] = 0) {
sum--;
}
if (oldColor = arr[index - 1] && color == arr[index - 1]) {
sum++;
}
} else {
if (oldColor == arr[index + 1] && arr[index + 1] = 0) {
sum--;
}
if (oldColor = arr[index + 1] && color == arr[index + 1]) {
sum++;
}
if (oldColor == arr[index - 1] && arr[index - 1] = 0) {
sum--;
}
if (oldColor = arr[index - 1] && color == arr[index - 1]) {
sum++;
}
}
ans[i] = sum;
}
return ans;
}
}
|
T4 动态规划
不妨从另一个视角观察问题,即从所有叶子到根节点的路径和是相等的
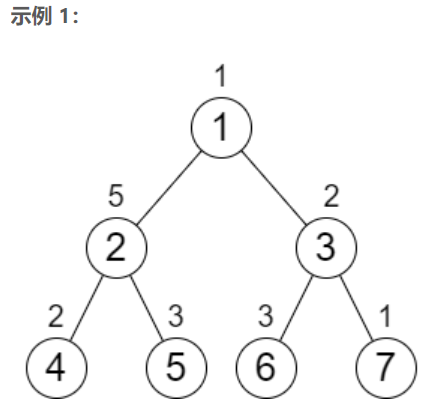
考虑下图中的编号为 4,5 的叶节点,不难发现,它们的所有祖先节点都是相同的,所以当它们的值相等时,到达根节点的路径和也是相等的。于是更新 4 号节点的值为两者间的较大值,并且将此时的值加到父节点的值上。对第 3 层的每对父节点相同的叶子节点进行同样的操作;再接着考虑第 2 层的两个节点,由于它们各自的子节点的值已经加上去了,所以此时第 2 层的内节点可以看成是新的叶节点,进行上面相同的操作;整个过程是一个动态规划的过程,省去了递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public int minIncrements(int n, int[] cost) {
int[] arr = new int[n + 1];
arr[0] = -1;
for (int i = 0; i < cost.length; i++) {
arr[i + 1] = cost[i];
}
int layer = (int) (Math.log(n + 1) / Math.log(2));
int ans = 0;
for (int i = layer; i >= 2; i--) {
int start = (int) Math.pow(2, i - 1);
int end = (int) Math.pow(2, i) - 1;
for (int j = start; j <= end - 1; j += 2) {
int val1 = arr[j];
int val2 = arr[j + 1];
int val = Math.max(val1, val2);
ans = ans + (val - val1) + (val - val2);
int parentIndex = (int) j / 2;
arr[parentIndex] += val;
}
}
return ans;
}
}
|
由于题目指明为满二叉树,所以可以方便地计算层数、父节点的索引
